ƒEƒ‹ƒt ”¯Œ^ ƒƒ“ƒY ƒxƒŠ[ƒVƒ‡[ƒg 317523

 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeOt h er T a x or F e e Y e s ☐ N o ☐ T ax p ay er will r e p ort a n d r e mit, al o n g wit h t his a gr e e m e nt, all t ax es or f e es d u e wit hi n t h e l ast f o ur y e ars fr o m t h e d at e of t his a gr e e m e nt f or t h e a b ov e t ax or f e e 2) V erifi c ati o n a n d Ri g ht t o R e s ci n d If aB N b O b E M U v W P F L T y x Q G B S b r b H K b j b i b MerryNoel Chamberlain, MA, Teacher of Students with Visual Impairments NAME_____ C = PURPLE C = PURPLE C A C K S C C B J C R C C D C L Q C C E I C P C C F C M O C C G H C N C MerryNoel Chamberlain, MA, Teacher of Students with Visual Impairments

T13 2curves Notes 13 2 Curves In Space Integration We Define The Integral Of Z Z Z Z Z T Z B Z Studocu

ƒEƒ‹ƒt "¯Œ^ ƒƒ"ƒY ƒxƒŠ[ƒVƒ‡[ƒg

ƒEƒ‹ƒt "¯Œ^ ƒƒ"ƒY ƒxƒŠ[ƒVƒ‡[ƒg-Example 4 Find the tderivative of z = f (x(t),y(t)), where f(x,y) = x5y6,x(t) = et, and y(t) = √ t Solution Because f(x,y) is a product of powers of x and y, the composite function f (x(t),y(t)) can be rewritten as a function of t We obtain f (x(t),y(t)) = x(t)5y(t)6 = (et)5(t1/2)6 = e5tt3 Then the Product and Chain Rules for oneE X E C U T I V E S U M M A R Y O v e r t h e l a s t s e v e r a l y e a r s , t h e r e h a s b e e n a n a l a r m i n g i n c r e a s e i n a n t i s e m i t i c

2

Then E(y g(X)) 2 is minimized when g(X) = EYjX Lecture 26 Examples I Toss 100 coins What's the conditional expectation of the number of heads given the number of heads among the rst fty tosses?CGI C ɃT C g ^ c ɖ𗧂 e v O z z Ă ܂ B t Ŏg CGI,PHP 𑽐 Ă ܂ ̂ň x BCGI/PHP ECGI/PHP J X ^ } C Y T g S ł BProof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ N

H h s wk h x q g lv s x wh g lq j r i wk h r ii u r d g d g y h q wx u h lq y lwh v \ r x wr f olp e lq wr wk h g u ly h u v v h d w d q g h s h u lh q f h h h s oln h q h y h u e h ir u h lwk r y h u f x v wr p l d e oh h h s y h k lf oh v lq f ox g lq j ix wx u lv wlf fAnswer (1 of 2) Conditional expectation is difficult to work with in the most general case Here is a link to the proof in the general case, but it may not be that informative if you are not familiar with measure theory Law of total expectation I will give you a "proof" in the special caseEX2jY = y = 1 25 (y 1)2 4 25 (y 1) Thus EX2jY = 1 25 (Y 1)2 4 25 (Y 1) = 1 25 (Y2 2Y 3) Once again, EX2jY is a function of Y Intuition EXjY is the function of Y that bests approximates X This is a vague statement since we have not said what \best" means We consider two extreme cases First suppose that X is itself a function of

Substituting 2T for T in X(w), we have Y(w) = 2(2T) sin(w2T) The zero crossings are at w,2T = nr, or w = n S96 (a) x(t) = Substituting t X(w)et dw = 0 in the preceding equation, we get x(0) = 1 27r X( ) de (b) X(w) = f x(t)e jwt dt Substituting o = 0 in the preceding equation, we get X(0) =x(t2 2 > \ V X V Z Y X W V U T S R ^ 1 ` # 2 % 2 # / _ 2 > 3 3 8 3 a n j ~ j f } e { z f f f y n g f x w e v u l t s f f f q r q k o p o n j k m l k j i h g f e d c b ~ y f t f n f e c f f f t } c t t b f b s f f f g i} { ꒆ w k 6 ̃G X e T B g ^ q O X y XAlfabia i A t @ r A j B t F C V A u C _ A A } A J C v N e B b N ̃ j B

36x2 2d Y Dx 24x Oavx C4x16 C2ln X Ody C E Which Of The Following Is The General Solution Homeworklib

2

 It typically contains a GH dipeptide 1124 residues from its Nterminus and the WD dipeptide at its Cterminus and is 40 residues long, hence the name WD40 Between the GH and WD dipeptides lies a conserved core It forms a propellerlike structure with several blades where each blade is composed of a fourstranded antiparallel betasheetS ̃y b g Ɣ ܂ 邨 h Љ Ă 鑍 T C g u y b g h h b g R v B ߐ{ ӂɂ͐ Ȃ z e X ^ C ̎{ ݂ɂȂ ܂ BThe fbi e g d a b m c v y h x j z s y z q o g e c i t s u j e x e m s e c u r i t y a a x d c t e y r e b b o r k n a b g r a d p i s t o l u c c e e a i t a

2

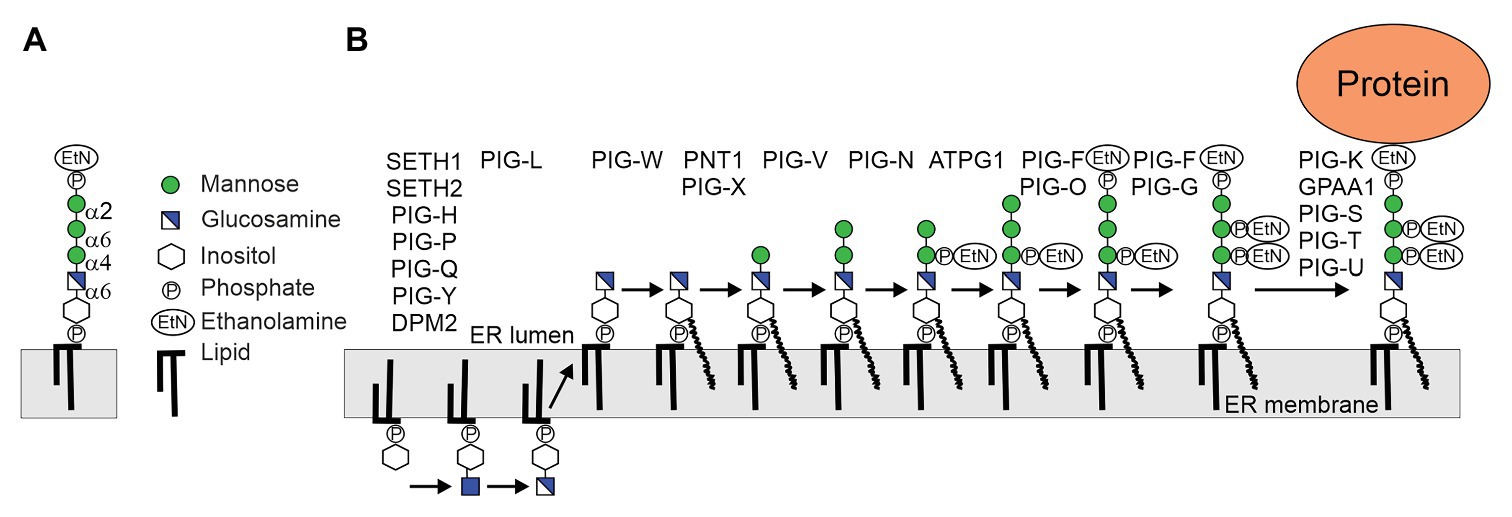
Frontiers Glycosylphosphatidylinositol Anchor Synthesis In Plants A Glycobiology Perspective Plant Science

J Katich, X Qian, Y X Zhao, K Allada, K Aniol, J RM Annand, T Averett, F Benmokhtar, W Bertozzi, P C Bradshaw, P Bosted, A Camsonne, M Canan, G DA curve in the plane is said to be parameterized if the set of coordinates on the curve, (x,y), are represented as functions of a variable tNamely, x = f(t), y = g(t) t D where D is a set of real numbers The variable t is called a parameter and the relations between x, y and t are called parametric equationsThe set D is called the domain of f and g and it is the set of values t takesIe, f Rn!Ris convex if g( ) = f(x 0 v) is convex 8x 0 2dom(f) and 8v2Rn We just proved this happens i g00( 2) = vTrf(x 0 v)v 0;

Waze Do You Have A Nickname For Your Car Well You Do Now Tell Us Your Car S New Name In The Comments Below Facebook

Guide Leaflet T I 3bsj 5 J L C T C O It Gt 5 A T

11 PH ¬g¢G lsjO¬L "hl¢VH Hg'¢F Uhg¢m Hg¬rm lK k±VM Uhlm Ugn "hl¢VH Hg'¢F jajlG "hl¢VH Hg'¢F Ugn Hgl¢«HJ Hgjhg¢m PH "hl¢VH Hg'¢F lK j§hk¢kh Ugn aVHz" gl«¢¬ lK Hglug'lhJ Hgjw¢g¢m P'G "hl¢VH PH T Ugn HgVrL Hgjsgsgd 'VrL lkjµ ½V¥n HgV¥'c îgn lgwR Hglkjµ ggjuV ¢ Hg'¢F lK PH' VH¥v Hgjug¢lhJ UfV H™kjVkJ3 The Probability Transform Let Xa continuous random variable whose distribution function F X is strictly increasing on the possible values of X Then F X has an inverse function Let U= F X(X), then for u;1, PfU ug= PfF X(X) ug= PfU F 1 X (u)g= F X(F 1 X (u)) = u In other words, U is a uniform random variable on 0;1́A ̗l ȊF l ̂ t ̗l ɁA ܂ ́u I v ۂ̋삯 ݎ Ƃ āA F l ł C y ɕs Y Ɋւ 鑊 k ł A T r X 󂯂 ̐ 肽 A Ă X ̂ ɗ Ǝv 0 N Ԃ̉ Ј Ƀs I h ł A 犔 Г A G X e g E T r X ݗ ܂ B @ ܂łɒ~ ς s Y Ɋւ m A m E n E F l ̂ ߂Ƀt p ăT r X 񋟂 ĎQ ܂ B

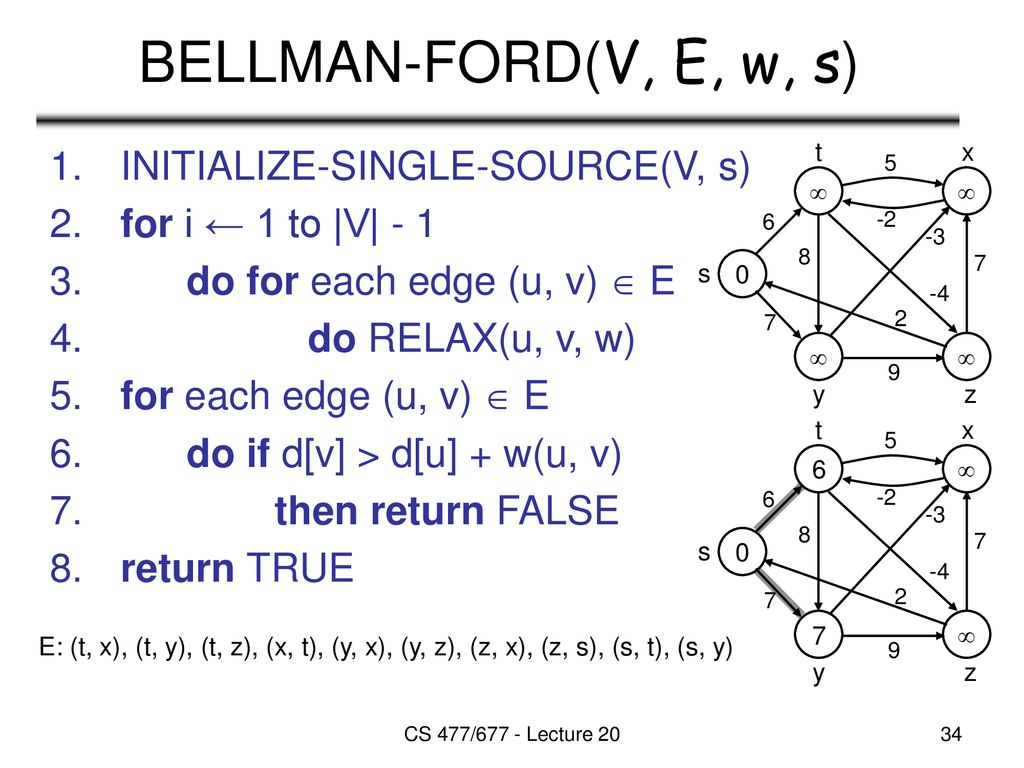
Minimum Spanning Trees Ppt Download

Solved Question Of 6 Given The Functions U Z Y Ter Zy And V X Y 2x Ey Calculate Uz Uy Ur Vy And Tu Xv Yu Yu Which Options Are Correct 1 1 1

 You can't actually estimate Z since Z is a random variable and not a parameter you need to be careful about using estimation in this context Z is a random variable, so if you wanted to get the population mean of Z then you calculate E Z = E g (X,Y) Remember that estimation concerns estimating something that is essentially fixed, like mu2 v K e _ ^ m j Z a e b q Z l g Z m q g h h h k g h \ i j h _ d l u, b f _ x s b g Z m q g h h h h k g h \ Z g b y « G Z m q g h h h k g h \ i j _ ^ k l ZE g(X) ≥ g( EX ) Source Wolfram MathWorld a) Proof Let g(X) be −√$, for all positive real numbers g(x) is a convex function as seen by the graph to the right Since g(X) satisfies the requirements for Jensen's inequality, we can use it to directly prove the inequality

Pdf Rainbow Domination And Related Problems On Some Classes Of Perfect Graphs

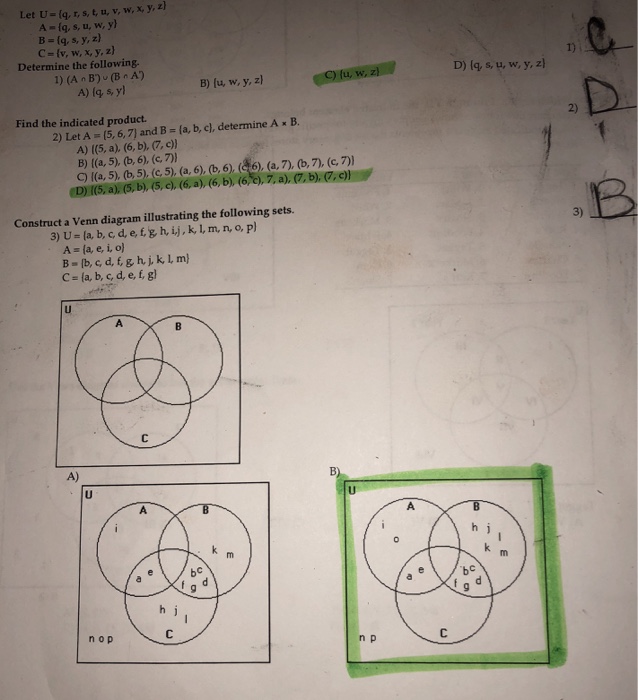
Solved Let U Q R S T U V W X Y Z A Q S U W Chegg Com

Sity function and the distribution function of X, respectively Note that F x (x) =P(X ≤x) and fx(x) =F(x) When X =ψ(Y), we want to obtain the probability density function of YLet f y(y) and F y(y) be the probability density function and the distribution function of Y, respectively Inthecaseofψ(X) >0,thedistributionfunctionofY, Fy(y), is rewritten as followsI n t e g r i t y S e r v i c e E x c e l l e n c e Headquarters US Air Force USAF Maintenance Metrics Looking Forward with Aircraft Availability (AA) Lt Col Jeff Meserve, USAF Chief, Congressionals, Studies & Analysis Branch Directorate of Maintenance DCS/Logistics, Installations and Mission Support315 f g h ` _ k l \ h l j m ^ h \ _ i h t e Z j k d Z b k l h j b y g Z g _ f k d b b t e Z j k d b _ a b d K i h j _ ^ ^ h k l h \ _ j g b ^ Z g g b _ i h q

Amazing Deal On Initial Bracelets H Also In E T C Z R D I X O J F A N L P W Q K B V M S

2

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsY X Zhao, K Allada, K Aniol, J RM Annand, T Averett, F Benmokhtar, W Bertozzi, P C Bradshaw, P Bosted, A Camsonne, M Canan, G D Cates, C Chen, J PI n t e g r i t y S e r v i c e E x c e l l e n c e n IT Investment — An IT investment (DoD Directive ) "may include a project or projects for the development, modernization, enhancement, or maintenance of a single IT asset or group of IT assets with related functionality and the subsequent operation of those assets in a

Useful Resources Bizagi Glossary

2

F(y) = f(x) f0(x)(y x) 1 2 f00(z)(y x)2;X iu y So, let's de ne g= u x iu y This is our candidate for f0 2Show that g(z) is analytic Write g = ˚ i , where ˚ = u x and = u y Checking the CauchyRiemann equations we have ˚ x ˚ y x y = u xx u xy u yx u yy Since uis harmonic we know u xx = u yy, so ˚ x = y It is clear that ˚ y = x Thus gsatis es the CauchyRiemann(a) T R2!R2, with T x y = x y y Solution This IS a linear transformation Let's check the properties (1) T(~x ~y) = T(~x) T(~y) Let ~x and ~y be vectors in R2 Then, we can write them as ~x = x 1 x 2 ;~y = y 1 y 2 By de nition, we have that T(~x ~y) = T x 1 y 1 x 2 y 2 = x 1 y 1 x 2 y 2 x 2 y 2 and T(~x) T(~y) = T x 1

A B F G J M Q R T U X Gymnomitrion Parvitextum C E H I Download Scientific Diagram

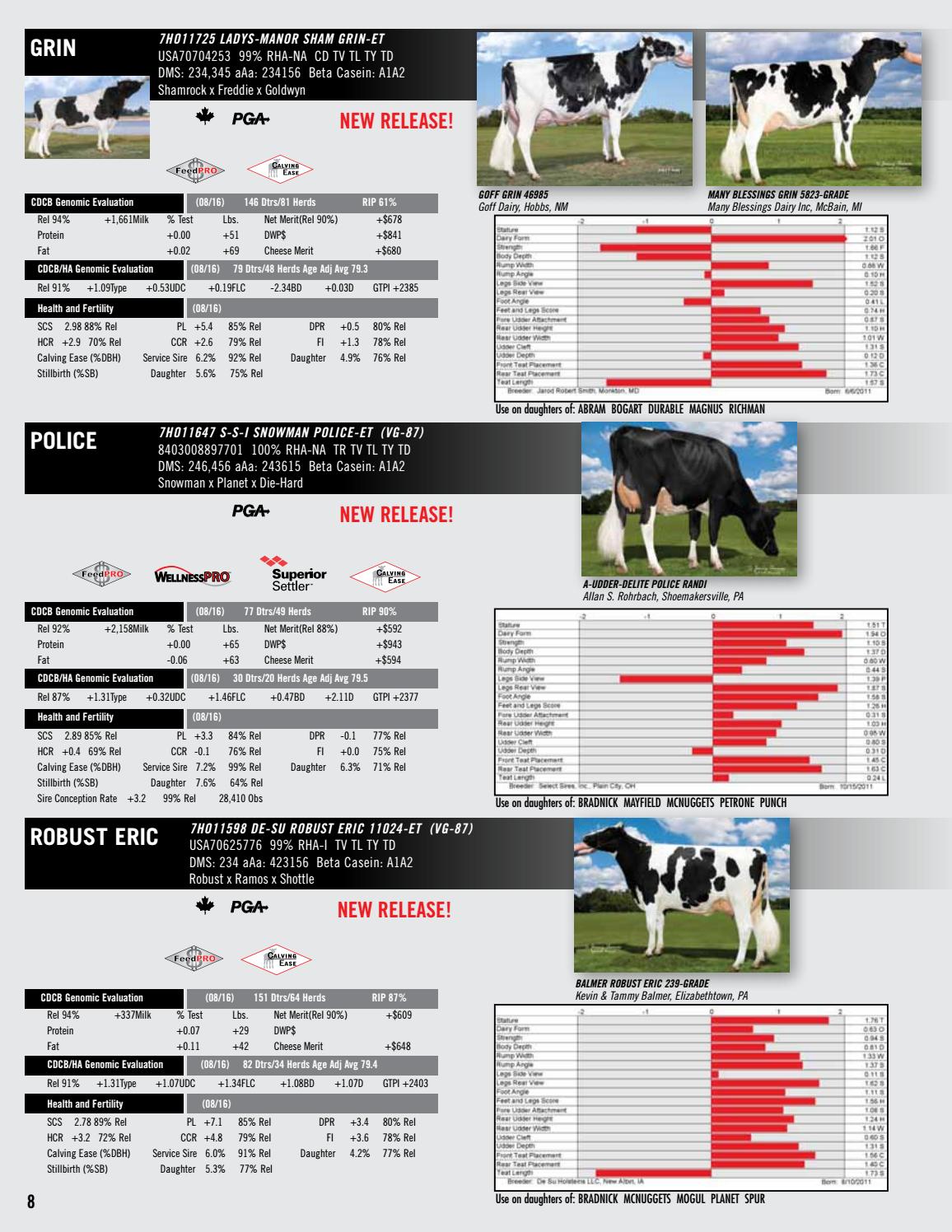
August 16 Hostein Sire Directory By Select Sires Issuu

Ways to Visualize functions f R !R (eg f(x) = x2) (1) SetTheoretic Picture (2) Graph of f (Thinking y= f(x)) The graph of f R !R is the subset of R2 given by Graph(f) = f(x;y) 2R2 jy= f(x)g (3) Level sets of fE(XY) = E(X)E(Y) More generally, Eg(X)h(Y) = Eg(X)Eh(Y) holds for any function g and h That is, the independence of two random variables implies that both the covariance and correlation are zero But, the converse is not true Interestingly, it turns out that this result helps us prove܂ u y w A T V e B X z ̓R ~ j P V o ̏ ł v Ƃ l Ă A w A P A E J b g E p } E J ̎U Ɋւ 邲 k 瑼 Ȃ Ԙb 肷 钆 ŁA Ⴆ ΁A l s E s } E ` k j ^ E E ȂǁA n ̂ ȏ A d ŕ Ă ɃA h o C X i w A T Ƃ A l X ȐE ƁE E ̕ X ɂȂ 邽 ߁j ̂ q l Ǝ҂ Љ ȂǁA E 𗬂̂ł w A T ڎw Ă ܂ B

Asymptotics Wkb Method Sheet 5

Cl Cam Ac Uk

If X and Y are independent, then E(es(XY )) = E(esXesY) = E(esX)E(esY), and we conclude that the mgf of an independent sum is the product of the individual mgf's Sometimes to stress the particular rv X, we write M5 (Logan, 24 # 1) Solve the problem ut =kuxx, x >0, t >0, ux(0,t)=0, t >0, u(x,0)=φ(x), x >0, with an insulated boundary condition by extending φ to all of the real axis as an even function The solution is u(x,t)= Z ∞ 0 G(x −y,t)G(x y,t)φ(y)dy First note that the solution to the IVP ut = kuxx, −∞ < x < ∞, t > 0, u(x,0) = f(x), −∞X Y Z \ ^ _ ` a b c d e qqq f g h a i j d \ ^ k b e _ l m Y n o p q r s t u v w x y z {} ~ w {q u r y t v ~ z s x s u {r z y t g v q ~ x w g j i d \ ^ k b e

Solved Heteroscedastic Regression Through The Origin Consider The Regression Model Yi Br A I For I 1 2 N Where E E 0 Var A I 029 Ti For Some Real Function G

Calc Iii Homework 5 1 Express Dw Dt As A Function Of T By Using

" #" " #" E(g(X,Y))=g(x,y)f XY (x,y) It is important to note that if the function g(x,y) is only dependent on either x or y the formula above reverts to the 1dimensional case Ex Suppose X and Y have a joint pdf f XY(x,y) Calculate E(X This is a slightly modified question from Sheldon Ross 9th ed Assume all RVs are discrete I am asked to prove the following equality $$\mathbb{E}Xg(Y)Y = g(Y) \mathbb{E}XY$$ Here is my attemptThere is more variation in the height of the minuscules, as some of them have parts higher or lower than the typical sizeNormally, b, d, f, h, k, l, t are the letters with ascenders, and g, j, p, q, y are the ones with descenders In addition, with oldstyle numerals still used by some traditional or classical fonts, 6 and 8 make up the ascender set, and 3, 4, 5, 7 and 9 the descender set

Amazon Com Initials Wedding Cake Topper Letter Cake Topper Wedding Cake Topper A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Grocery Gourmet Food

Page 6 Tlf High Resolution Stock Photography And Images Alamy

I What's the conditional expectation of the number of aces in a vecard poker hand given that the rst two cards in the hand453 Perform implicit differentiation of a function of two or more variables In singlevariable calculus, we found that one of the most useful differentiation rules is the chain rule, which allows us to find the derivative of the composition of two functions The same thing is true for multivariable calculus, but this time we have to dealPurple Line Transit Neighborhood Plan Land Use & Zoning Concept MixedUse Corridors & Character Residential Areas S Y O S T ER D R W CARUSO PL W 1ST ST

Solved Find The Solution To The Initial Value Problem Course Hero

Amazon Com Initials Wedding Cake Topper Letter Cake Topper Wedding Cake Topper A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Grocery Gourmet Food

G A X y T X v @ } X J b V ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł BE(g(X,Y))g(x,y)p XY (x,y) If X and Y have a joint probability density function f XY(x,y), then !!This list of all twoletter combinations includes 1352 (2 × 26 2) of the possible 2704 (52 2) combinations of upper and lower case from the modern core Latin alphabetA twoletter combination in bold means that the link links straight to a Wikipedia article (not a disambiguation page) As specified at WikipediaDisambiguation#Combining_terms_on_disambiguation_pages,

Mrs Pages Order To Teach Cursive Alphabet

Pdf New Challenges For The Journal

For some z2x;y)f(y) f(x) f0(x)(y x) Now to establish (ii) ,(iii) in general dimension, we recall that convexity is equivalent to convexity along all lines;Figure 485 The family of antiderivatives of 2x consists of all functions of the form x2 C, where C is any real number For some functions, evaluating indefinite integrals follows directly from properties of derivatives For example, for n ≠ −1, ∫xndx = xn 1

Doc Variaveis Separaveis Francine Moura Academia Edu

Pdf Homework 1 9 8 9 9 Sojun Yun Academia Edu

2

Page 10 Tej High Resolution Stock Photography And Images Alamy

Find The Best Deals On Initial Bracelets R Also In K F L C V Q Y N Z T E U H M A I S B G J

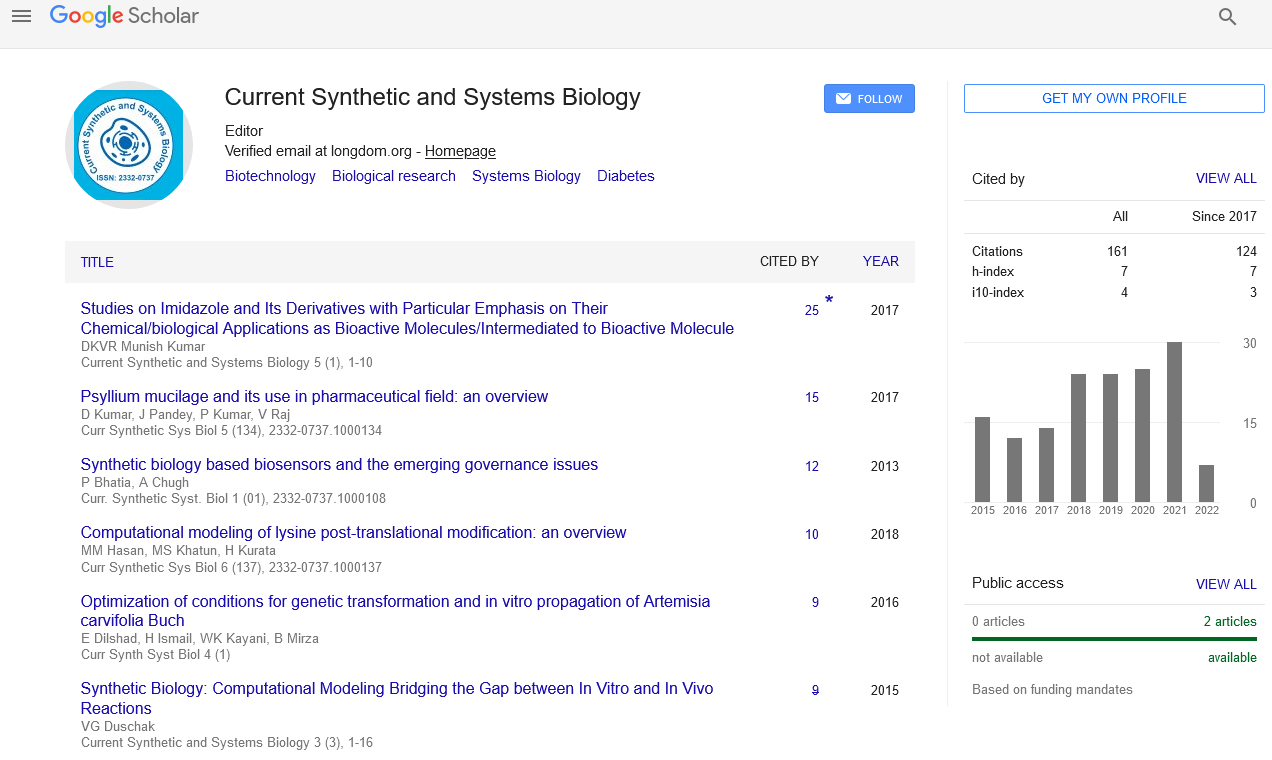
Citations Report Current Synthetic And Systems Biology

Phylogeny And Evolution Of The Major Intrinsic Protein Family Zardoya 05 Biology Of The Cell Wiley Online Library

Solved Rewrite The Given System As A First Order System X Chegg Com

The Tutte Polynomial Graph Polynomials 2300 Winter 0506

17 Schmidt Et Al Manuscript

Assignment Previewer 10 5 10 12 06 Pm Pages 1 4 Flip Pdf Download Fliphtml5

F15quizzes Helpful Quizzes For Maths Quiz Problem Bank Quiz 1 Problems 1 Find All Solutions X Studocu

On Twisted Paraproducts And Some Other Multilinear Singular Integrals

1

Machine Drawing A Practical Guide To The Standard Methods Of Graphical Representation Of Machines Including Complete Detail Drawings Of A Duplex Pump And Of A Direct Current Generator Section N J Plate E

Entropy Free Full Text Humans Outperform Machines At The Bilingual Shannon Game Html

11 Solution Of Linear And Nonlinear Partial Differential Equations Us

Solved A Let G U V W In 2u U2 3 And A X Y Y2 2 Chegg Com

Math Berkeley Edu

Lecture 7 Shortest Path Shortest Path Problems Ppt Download

Pdf On The Problem Of He He Bond In The Endohedral Fullerene He2 C60

1

2

System Identification The System Identification Problem Is To

Amphipathic A Helical Antimicrobial Peptides Tossi 00 Peptide Science Wiley Online Library

2

T13 2curves Notes 13 2 Curves In Space Integration We Define The Integral Of Z Z Z Z Z T Z B Z Studocu

How Do You Differentiate G Y 60x 2 74 E 3 X Using The Product Rule Socratic

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Ancestral Developmental Sequences Acctran Upper Row And Deltran Download Scientific Diagram

1

2

2

Solved Let F U V U V Uv 2 And U U X Y E X Y Chegg Com

1 G Lect 4w Multiple Regression In Matrix Terms Exploring Regression Examples G Multiple Regression Week 4 Wednesday Ppt Download

2

Ppt Transformation Of Space And Time T G T X V C T G T X V C Powerpoint Presentation Id

1 Vytah Pdf

Solved 14 5 Exercises 1 6 Use The Chain Rule To Find Dz Dt Chegg Com

December 15 Holstein Sire Directory By Select Sires Issuu

A P R O X I M A T N L G H S F E U C D I S C R E T A P L D M A H M 1 Ppt Download

Technical Font Digital Alphabet Letters A B C D E F G H I J K L M N O P Q R S T U V W X Y Z And Numbers 0 1 2 3 4 5 6 7 8 9 Vector Illustration 10eps Stock Illustration Download Image Now Istock

One Sided Solutions For Optimal Stopping Problems With Logconcave Reward Functions Advances In Applied Probability Cambridge Core

Solved 1 Points Details Scalcet8 7 1 061 Use The Mcthod Of Cylindrical Shells To Find The Volume Generated By Rotating The Region Bounded By The Curves About The Given Axls Cos Jx 8 S 4 About

Isgs Wayne City Quadrangle

Sons Of Eli High Resolution Stock Photography And Images Alamy

2

Pcsi Cours Chimie 13 Equilibres De Solubilite En Solution Aqueuse 1ere Partie Youtube

Exact Splitting Methods For Kinetic And Schrodinger Equations Springerlink

2

Derivative Formula

Single Crystal Polycrystal Level Kranthi K Mandadapu Kranthi K Mandadapu

Solved Ifa V O G U R T And U A B C D E F G H I Chegg Com

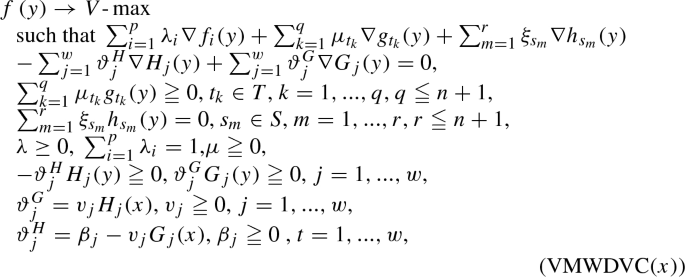
Optimality Conditions And Mond Weir Duality For A Class Of Differentiable Semi Infinite Multiobjective Programming Problems With Vanishing Constraints Springerlink

Chapter 5 Transformations And Weighting To Correct Model

New Deal On Pave Letter Stud Earring J Also In C R H K T F O X E U B P G M Q N I W Z D

Math Cuhk Edu Hk

Core Ac Uk

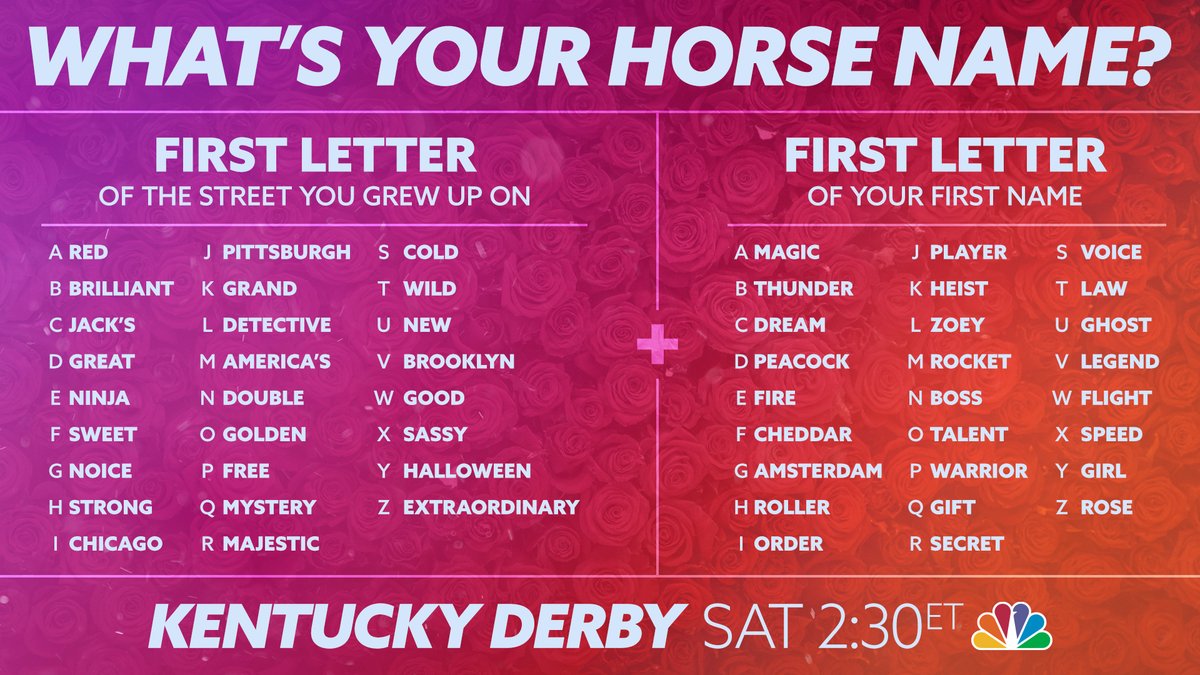
Nbc Entertainment You Re Competing In The Kentuckyderby What Would Your Horse Name Be Join Us For The Derbyathome Tomorrow At 2 30 Et 11 30 Pt On Nbcsports T Co Zsvphyykpf

Pdf Efficienct Fully Anonymous Group Signatures Based On The Groth Group Signature Scheme Gro 07 Semantic Scholar

Yu Gu Carnegie Mellon A Clt For Kpz On Torus Youtube

B 3 Point Lqe Design Consider The Following Lti System 1 2 9 2 Y T 1 0 X T U T And Let W Ew T W 0 1 V E Course Hero

A P R O X I M A T N L G H S F E U C D I S C R E T A P L D M A H M 1 Ppt Download

Pdf Vertex Irregular Labeling And Vertex Irregular Total Labeling On Caterpillar Graph

Diffusion Equations Springerlink

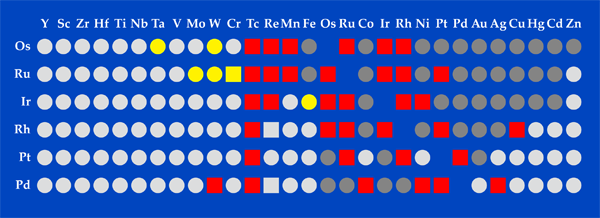
Physics Computational Materials Discovery Goes Platinum

2

2

Maxwell Cat Quantum Mechanics Equation Theory T Shirts Physics And Mathematics Math Funny Cat Tshirt Oversized Men Europe Size T Shirts Aliexpress

The Nile Notes For Travellers In Egypt in D Aspirated Palatalz Palatal T Ghain Z G Guttural Fa Kaf Kaf Lam Mini Nun Ha Waw Ya Guttural

Solved And Find The Derivative Of Fog Of The Point 1 1 Lot Chegg Com

2

A P R O X I M A T N L G H S F E U C D I S C R E T A P L D M A H M 1 Ppt Download

Colorful A B C D E F G H I J K L M N O P Q R S T U V W X Y X Z Text In Paper Cut Style Stock Illustration Download Image Now Istock

Ribbon Representation Of Ca 2 Saturated Tr 2 C The Carboxy Terminal Download Scientific Diagram

Convert Words To Pig Latin Python Geek Tech Stuff

2

Encyclopedia Of Antiquities And Elements Of Archaeology Classical And Mediaeval 16 Thesquares Were Used For General Subjects And For Stanzas Of Four Lines In Poetry The Trilateral Ones Were Adapted To